Asimetría y kurtosis

La asimetría y la kurtosis son dos conceptos estadísticos que describen la forma de la distribución de un conjunto de datos. Estos conceptos son útiles para entender cómo se distribuyen los datos en relación con una distribución normal. A continuación, se explican en detalle estos conceptos, sus propiedades, ejemplos y cómo calcularlos en Python.

1. Asimetría

¿Qué es la Asimetría?

La asimetría (o sesgo) es una medida de la simetría de la distribución de los datos. Describe cómo se distribuyen los valores en torno a la media.

• Asimetría positiva: Cuando la cola derecha de la distribución es más larga o tiene más peso que la cola izquierda. Esto indica que hay más valores extremos en el lado derecho.
• Asimetría negativa: Cuando la cola izquierda de la distribución es más larga o tiene más peso que la cola derecha. Esto indica que hay más valores extremos en el lado izquierdo.
• Asimetría cero: Cuando la distribución es simétrica, similar a una distribución normal.

Propiedades de la Asimetría

1. Interpretación:
   • Asimetría positiva: Media > Mediana > Moda.
   • Asimetría negativa: Moda > Mediana > Media.
   • Asimetría cero: Media = Mediana = Moda.
2. Rango de valores: La asimetría puede tomar valores entre -infinito e infinito.
3. Cálculo: Se puede calcular utilizando diferentes métodos, pero la fórmula más común es:

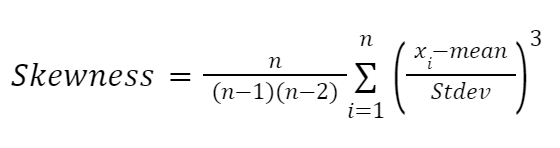
donde (n) es el número de observaciones, (x_i) son los valores, mean es la media y Stdev es la desviación estándar.

Ejemplo de Asimetría

Vamos a calcular la asimetría de un conjunto de datos utilizando Python.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew

data_l = np.array([1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 6, 8, 10])

# Imprimir los datos
print("Datos asimétricos a la derecha:")
print(data_l)

# Visualizar la distribución
plt.figure(figsize=(10, 6))
sns.histplot(data_l, bins=10, kde=True)
plt.title('Distribución Asimétrica a la Derecha')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.show()
asimetria = skew(data_l)
print(f"Asimetría: {asimetria:.2f}")

data_r = np.array([1, 3, 3, 7, 7, 7, 9, 9, 9, 9, 10, 10, 10, 10, 10])
# Visualizar la distribución
plt.figure(figsize=(10, 6))
sns.histplot(data_r, bins=10, kde=True)
plt.title('Distribución Asimétrica a la Izquierda')
plt.xlabel('Valor')
plt.ylabel('Frecuencia')
plt.show()
asimetria = skew(data_r)
# Imprimir los datos generados
print("Datos generados (sesgados a la izquierda):", data_r)
print(f"Asimetría: {asimetria:.2f}")

Interpretación de los valores de asimetría:

1. Asimetría cercana a 0:
   • La distribución es aproximadamente simétrica.
   • Valores en el rango de -0.5 a 0.5 se consideran simetría baja.
2. Asimetría positiva (skew positivo):
   • La cola derecha de la distribución es más larga o tiene más valores que la izquierda.
   • Valores de skew > 0.5 indican una distribución con una asimetría positiva considerable.
   • Ejemplo: Distribuciones de ingresos, donde la mayoría de las personas ganan cantidades más bajas y unos pocos ganan mucho.
3. Asimetría negativa (skew negativo):
   • La cola izquierda de la distribución es más larga o tiene más valores que la derecha.
   • Valores de skew < -0.5 indican una distribución con una asimetría negativa considerable.
   • Ejemplo: Distribuciones como la edad de jubilación, donde la mayoría se jubila alrededor de una cierta edad y pocas personas se jubilan muy jóvenes.

Rangos de referencia:

• Entre -0.5 y 0.5: Distribución casi simétrica.
• Entre -1 y -0.5 o 0.5 y 1: Sesgo moderado (negativo o positivo).
• Mayor que 1 o menor que -1: Sesgo alto (positivo o negativo).

Ejemplo:

• Skew = 0: Distribución perfectamente simétrica (como la distribución normal ideal).
• Skew = 2: Distribución con sesgo positivo significativo.
• Skew = -1.5: Distribución con sesgo negativo considerable.

En resumen, cuanto más se aleje el valor de la asimetría de cero, más sesgada estará la distribución.

2. Kurtosis

¿Qué es la Kurtosis?

La kurtosis es una medida que describe la “altura” y “ancho” de la distribución de los datos, en particular, se refiere a la “concentración” de los datos en las colas y en el centro de la distribución.

• Kurtosis alta (leptocúrtica): Las distribuciones con colas más pesadas que una normal. Indica que hay más valores extremos.
• Kurtosis baja (platicúrtica): Las distribuciones con colas más ligeras que una normal. Indica que hay menos valores extremos.
• Kurtosis normal: Una distribución normal tiene una kurtosis de 3.

Propiedades de la Kurtosis

1. Interpretación:
   • Kurtosis alta: Más datos en las colas, indicando un mayor riesgo de valores extremos.
   • Kurtosis baja: Menos datos en las colas, indicando menor riesgo de valores extremos.
2. Cálculo: La kurtosis se puede calcular con la siguiente fórmula:
3. 

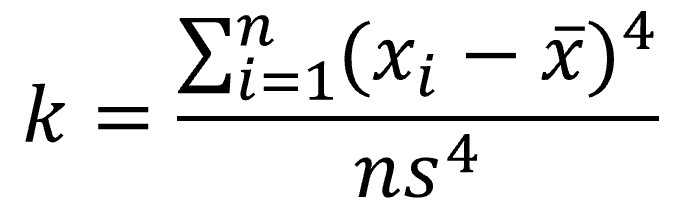
[ \text{Kurtosis} = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \sum \left( \frac{x_i – \bar{x}}{s} \right)^4 – \frac{3(n-1)^2}{(n-2)(n-3)} ]

donde (n) es el número de observaciones, (x_i) son los valores, x con barra es la media y (s) es la desviación estándar.

Ejemplo de Kurtosis

Calculemos la kurtosis de un conjunto de datos utilizando Python.

from scipy.stats import kurtosis

# Conjunto de datos
data = [10, 12, 12, 13, 12, 11, 15, 16, 20, 25]

# Calcular la kurtosis
kurtosis_value = kurtosis(data)
print(f"Kurtosis: {kurtosis_value:.2f}")

Resumen Completo en Python

Aquí tienes un bloque de código que incluye el cálculo tanto de la asimetría como de la kurtosis para un conjunto de datos.

import numpy as np
import pandas as pd
from scipy.stats import skew, kurtosis

# Conjunto de datos
data = [10, 12, 12, 13, 12, 11, 15, 16, 20, 25]

# Calcular la asimetría
asimetria = skew(data)
print(f"Asimetría: {asimetria:.2f}")

# Calcular la kurtosis
kurtosis_value = kurtosis(data)
print(f"Kurtosis: {kurtosis_value:.2f}")

Aquí un código que compara diferentes distribuciones con curtosis bajas, medias y altas:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import kurtosis


# Generar una distribución de Laplace
# La distribución de Laplace tiene colas más pesadas y una curtosis alta
mu = 0         # Media
b = 1          # Parámetro de escala
data = np.random.laplace(mu,b, size=1000)
print (kurtosis(data, fisher=False))

data_u=np.random.uniform(-10,10,1000)
print (kurtosis(data_u, fisher=False))

data_n=np.random.normal(0,5,1000)
print (kurtosis(data_n, fisher=False))

# Crear el gráfico
plt.figure(figsize=(10, 6))
sns.histplot(data, bins=30, kde=True, stat="density", color='blue', alpha=0.6)
sns.histplot(data_u, bins=30, kde=True, stat="density", color='green', alpha=0.6)
sns.histplot(data_n, bins=30, kde=True, stat="density", color='red', alpha=0.6)
plt.title('Distribuciones con diferentes curtosis')
plt.xlabel('Valores')
plt.ylabel('Densidad')
plt.grid(True)
plt.show()

Conclusión

La asimetría y la kurtosis son medidas estadísticas clave que proporcionan información valiosa sobre la forma de la distribución de los datos. La asimetría indica la simetría de la distribución, mientras que la kurtosis indica la concentración de los datos en las colas y el centro. Ambos conceptos son útiles para el análisis de datos y la toma de decisiones en diversos contextos.