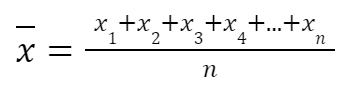Diferentes tipos de medias

1. Media

La media es una medida de tendencia central que se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado entre el número total de valores. Es útil para representar un valor “típico” de un conjunto de datos.

Fórmula

donde:

• (x_i) son los valores del conjunto de datos.
• (n) es el número total de valores.

Ejemplo

Consideremos el siguiente conjunto de datos: 5, 10, 15, 20, 25.

Cálculo:

Código en Python

import numpy as np

# Conjunto de datos
data = np.array([5, 10, 15, 20, 25])

# Cálculo de la media
mean = np.mean(data)
print(f"Media: {mean}")

2. Media Ponderada

La media ponderada es similar a la media, pero en este caso, cada valor en el conjunto de datos tiene un peso asociado que indica su importancia relativa. Es útil cuando algunos valores deben contribuir más al resultado final que otros.

Fórmula

donde:

• (x_i) son los valores del conjunto de datos.
• (w_i) son los pesos asociados a cada valor.
• (n) es el número total de valores.

Ejemplo

Consideremos el siguiente conjunto de datos: 5, 10, 15, 20, 25 con pesos: 1, 2, 3, 4, 5.

Cálculo:

[ \text{Media Ponderada} = \frac{(1 \cdot 5) + (2 \cdot 10) + (3 \cdot 15) + (4 \cdot 20) + (5 \cdot 25)}{1 + 2 + 3 + 4 + 5} = \frac{(5 + 20 + 45 + 80 + 125)}{15} = \frac{275}{15} \approx 18.33 ]

Código en Python

# Conjunto de datos y pesos
data = np.array([5, 10, 15, 20, 25])
weights = np.array([1, 2, 3, 4, 5])

# Cálculo de la media ponderada
weighted_mean = np.average(data, weights=weights)
print(f"Media Ponderada: {weighted_mean}")

3. Media Truncada

La media truncada es una medida de tendencia central que se calcula eliminando un porcentaje de los valores más extremos (superiores e inferiores) de un conjunto de datos antes de calcular la media. Es útil para minimizar el efecto de los valores atípicos en la media.

Fórmula

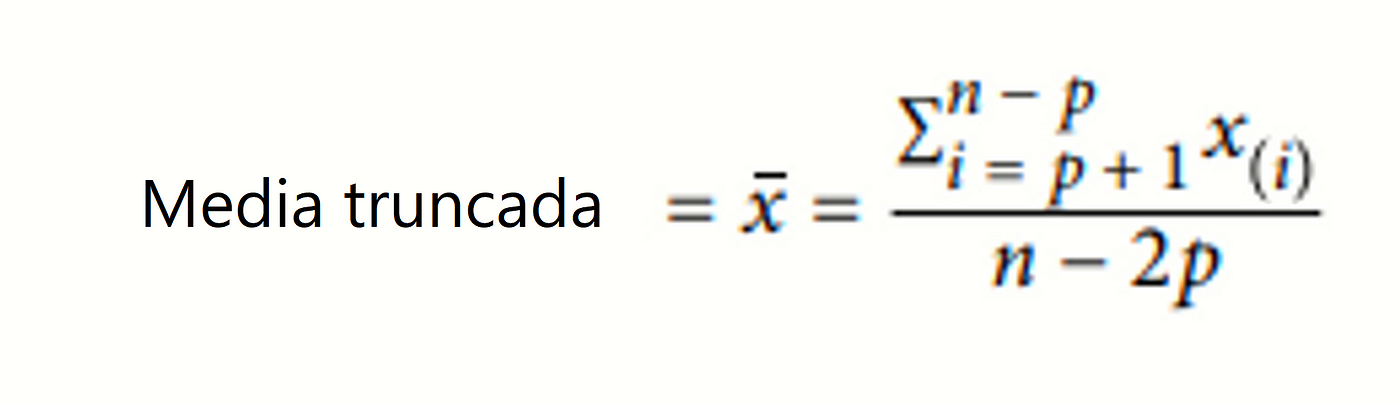
donde:

• (m) es el número de valores eliminados de cada extremo.

Ejemplo

Consideremos el siguiente conjunto de datos: 5, 10, 15, 20, 25, 100 (donde 100 es un valor atípico). Si decidimos truncar el 20% de los datos, eliminamos el 20% más bajo (5 y 10) y el 20% más alto (100).

Datos después de truncar: 15, 20, 25.

Cálculo:

Media Truncada (15 + 20 + 25)/3 = 60/3 = 20

Código en Python

def truncated_mean(data, proportion):
    # Ordenar los datos
    sorted_data = np.sort(data)
    # Calcular cuántos elementos truncar
    n = len(data)
    trim_count = int(n * proportion)
    # Calcular la media truncada
    truncated_data = sorted_data[trim_count:n - trim_count]
    return np.mean(truncated_data)

# Conjunto de datos
data = np.array([5, 10, 15, 20, 25, 100])

# Cálculo de la media truncada (20% de truncamiento)
truncated_mean_value = truncated_mean(data, 0.2)
print(f"Media Truncada: {truncated_mean_value}")

Conclusión

• La media es una medida simple y directa, pero puede ser afectada por valores atípicos.
• La media ponderada permite que algunos valores tengan más influencia en el cálculo final, lo cual es útil en muchos contextos.
• La media truncada es útil para reducir el impacto de valores extremos y obtener una representación más robusta del centro de los datos.