Funciones de activación

Las funciones de activación en redes neuronales transforman la entrada de una neurona en una salida, introduciendo no linealidades en el modelo. Esto permite que la red capture relaciones complejas entre los datos, haciendo que pueda resolver problemas que van más allá de simples combinaciones lineales. A continuación, explico algunas de las funciones de activación más comunes, junto con sus características y ejemplos de uso:

1. Función Sigmoide (Sigmoid)

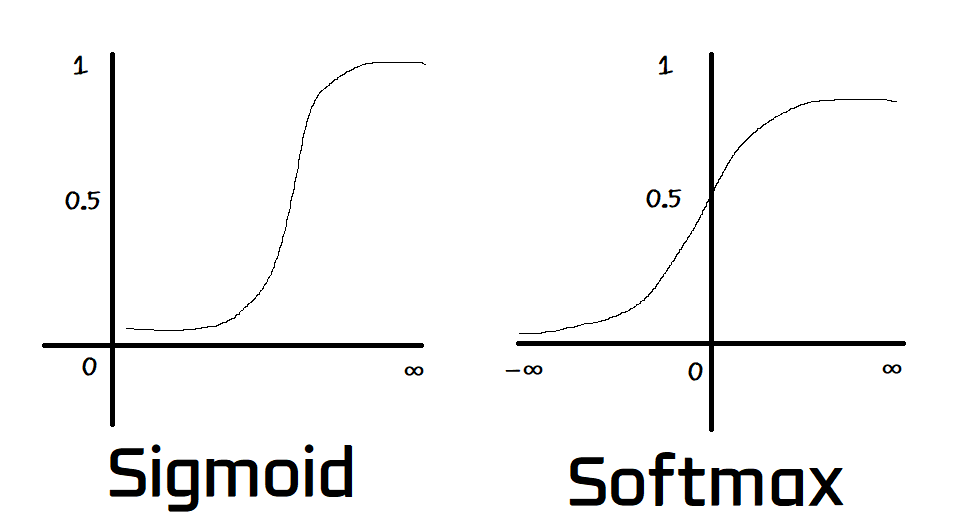
La función sigmoide mapea valores de entrada en un rango entre 0 y 1. Es adecuada para modelos en los que se necesita una salida probabilística.

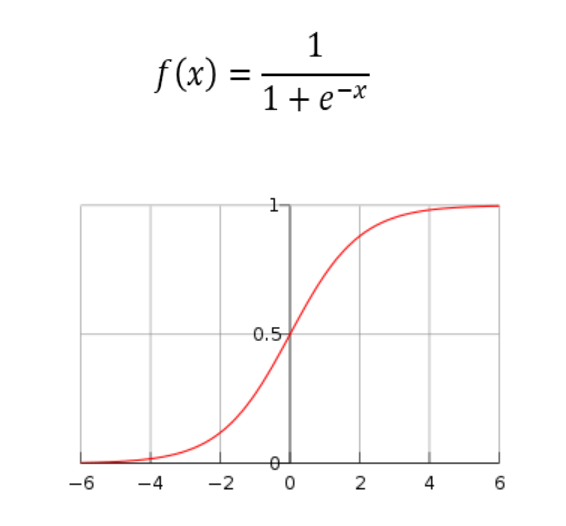
Ejemplo de uso: La función sigmoide es común en la última capa de redes neuronales para clasificación binaria, ya que convierte la salida en una probabilidad.

import numpy as np
import matplotlib.pyplot as plt

# Valores de entrada
x = np.linspace(-10, 10, 100)
# Aplicamos la función sigmoide
sigmoid = 1 / (1 + np.exp(-x))

plt.plot(x, sigmoid)
plt.title("Función Sigmoide")
plt.show()

Ventajas: Buena para probabilidades y salida entre 0 y 1.
Desventajas: Su salida se satura en valores extremos, lo que puede causar problemas de gradientes vanishing (desaparecen gradientes) al entrenar redes profundas.

2. Función Tanh (Tangente Hiperbólica)

La función tangente hiperbólica mapea los valores de entrada a un rango entre -1 y 1. Es similar a la sigmoide, pero con un rango más amplio que la hace útil en redes profundas.

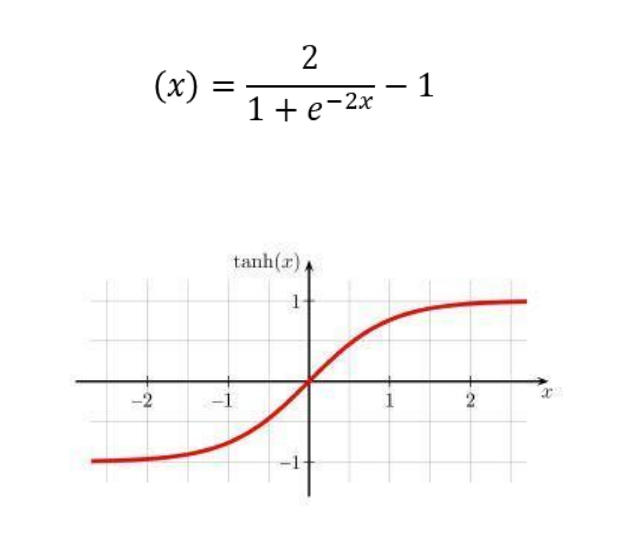
Ejemplo de uso: A menudo se usa en capas ocultas de redes neuronales porque sus valores centrados en cero facilitan la propagación de la señal hacia adelante y hacia atrás.

tanh = np.tanh(x)
plt.plot(x, tanh)
plt.title("Función Tangente Hiperbólica")
plt.show()

Ventajas: Ayuda a una mejor convergencia en redes profundas que la sigmoide.
Desventajas: Aunque reduce el problema del gradiente, sigue siendo susceptible a la saturación.

3. Función ReLU (Rectified Linear Unit)

ReLU es la función de activación más común en redes profundas, especialmente en redes convolucionales. Convierte valores negativos en cero y deja los positivos sin cambios.

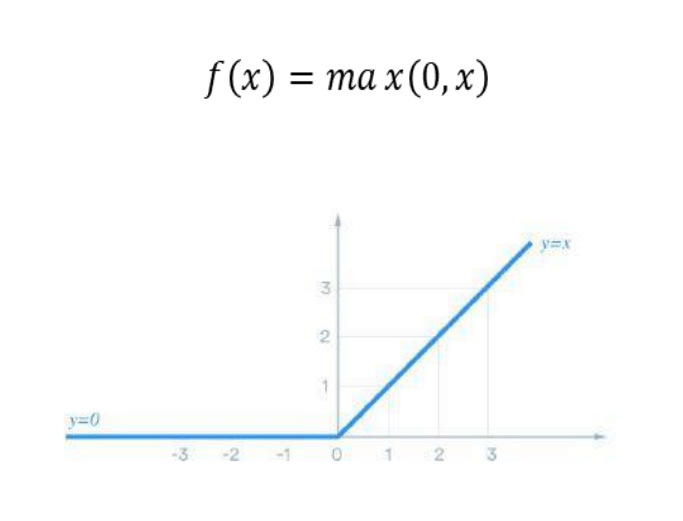
Ejemplo de uso: Se aplica en la mayoría de las capas ocultas debido a su capacidad para acelerar el aprendizaje al evitar saturación en valores positivos.

relu = np.maximum(0, x)
plt.plot(x, relu)
plt.title("Función ReLU")
plt.show()

Ventajas: Mitiga el problema de gradientes vanishing y mejora la eficiencia computacional.
Desventajas: Problema de neuronas muertas, ya que valores negativos se convierten en cero, y la neurona nunca se activa.

4. Función ReLU Leaky

La ReLU Leaky introduce un pequeño gradiente para valores negativos, mitigando el problema de las neuronas muertas en la ReLU convencional.

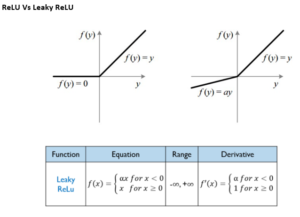
Ejemplo de uso: Es común en redes profundas donde la saturación de valores negativos podría limitar el aprendizaje.

leaky_relu = np.where(x > 0, x, 0.01 * x)
plt.plot(x, leaky_relu)
plt.title("Función ReLU Leaky")
plt.show()

Ventajas: Previene neuronas muertas.
Desventajas: Introduce un pequeño gradiente negativo, lo que a veces requiere ajuste.

5. Función Softmax

Softmax se usa principalmente en la última capa de una red neuronal para problemas de clasificación multiclase. Convierte una lista de valores en probabilidades que suman 1.

Ejemplo de uso: Es ideal para clasificación de múltiples categorías (por ejemplo, clasificación de imágenes en categorías distintas).

def softmax(x):
    e_x = np.exp(x - np.max(x))  # Para estabilidad numérica
    return e_x / e_x.sum(axis=0)

# Ejemplo de vector
x_softmax = np.array([1, 2, 3, 4, 5])
y_softmax = softmax(x_softmax)
plt.bar(range(len(y_softmax)), y_softmax)
plt.title("Función Softmax")
plt.show()

Ventajas: Proporciona una salida probabilística para problemas multiclase.
Desventajas: Computacionalmente costosa y susceptible a problemas de gradientes desvanecientes.

Estas funciones se pueden combinar de manera que cada capa de la red neuronal use una u otra según sea necesario para mejorar la capacidad de la red de generalizar patrones complejos en los datos.