Métodos estadísticos descriptivos

Métodos Descriptivos en Estadística

Los métodos descriptivos son un conjunto de herramientas estadísticas utilizadas para resumir, organizar y describir los datos de manera efectiva. El objetivo principal es presentar los datos de forma clara y concisa, permitiendo una rápida comprensión de las características esenciales de un conjunto de datos sin realizar inferencias o predicciones. Estos métodos se pueden aplicar a cualquier tipo de dato y son fundamentales en la primera etapa del análisis estadístico, también conocida como análisis exploratorio de datos (EDA).

Tipos de Métodos Descriptivos

Los métodos descriptivos se dividen en dos categorías principales:

1. Medidas de Tendencia Central: Estas medidas buscan identificar el punto central o el valor típico de un conjunto de datos.
2. Medidas de Dispersión o Variabilidad: Estas medidas describen cuán dispersos o agrupados están los datos en torno a un valor central.

Veamos cada categoría en detalle.

---

1. Medidas de Tendencia Central

Las medidas de tendencia central proporcionan un valor único que representa el centro de un conjunto de datos. Los métodos más comunes son:

a. Media Aritmética (Promedio)

La media aritmética es la suma de todos los valores dividida entre el número total de observaciones. Es la medida más utilizada para datos numéricos.

• Fórmula:
• 
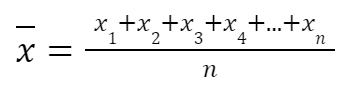
• Donde (X_i) son los valores de los datos y (n) es el número total de observaciones.
• Ejemplo: Si tenemos los siguientes datos sobre las calificaciones de un grupo de estudiantes: 8, 7, 9, 10 y 6, la media sería:
  (8 + 7 + 9 + 10 + 6)/5 = 8

b. Mediana

La mediana es el valor que divide a un conjunto de datos ordenados en dos partes iguales. Es útil cuando los datos tienen valores extremos (outliers) que distorsionarían la media.

• Cálculo: Si el número de observaciones es impar, la mediana es el valor en el centro. Si es par, es el promedio de los dos valores centrales.
• Ejemplo: En el conjunto de datos: 8, 7, 9, 10 y 6, primero ordenamos los datos: 6, 7, 8, 9, 10. La mediana es 8.

c. Moda

La moda es el valor o valores que aparecen con mayor frecuencia en un conjunto de datos. Es útil cuando se quiere identificar el valor más común.

• Ejemplo: En el conjunto de datos: 5, 8, 8, 10, 6, 8, la moda es 8, ya que es el valor que más se repite.

Cuándo usar cada una:

• Media: Para datos simétricos sin valores extremos significativos.
• Mediana: Para datos asimétricos o con outliers.
• Moda: Para datos categóricos o cuando es necesario identificar la frecuencia más común.

---

2. Medidas de Dispersión o Variabilidad

Mientras que las medidas de tendencia central describen el “centro” de los datos, las medidas de dispersión indican qué tan extendidos o compactos están los datos en torno a ese centro.

a. Rango

El rango es la diferencia entre el valor máximo y el mínimo de un conjunto de datos. Es una medida simple que proporciona una idea rápida de la variabilidad.

• Fórmula:
  Rango = Xmáx- Xmín
• Ejemplo: En el conjunto de datos: 6, 7, 8, 9, 10, el rango sería:
  [ 10 – 6 = 4 ]

b. Varianza

La varianza mide la dispersión de los datos con respecto a la media. Se calcula como la media de los cuadrados de las diferencias de cada valor respecto a la media.

• Fórmula:
• 
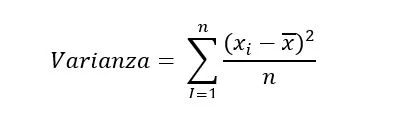
  Donde X es la media.
• Ejemplo: Para los datos 8, 7, 9, 10 y 6, primero se calcula la media ( \bar{X} = 8 ). Luego, se halla la varianza sumando los cuadrados de las diferencias entre cada valor y la media:
  [(8-8)^2 + (7-8)^2 + (9-8)^2 + (10-8)^2 + (6-8)^2]/5 = 2.5

c. Desviación Estándar

La desviación estándar es la raíz cuadrada de la varianza. Es una medida más intuitiva de la dispersión ya que está en las mismas unidades que los datos originales.

• Fórmula:
  Desviación Estándar = sqrt(Varianza)
• Ejemplo: Si la varianza es 2.5, la desviación estándar es:
  [ \sqrt{2.5} = 1.58 ]

d. Rango Intercuartílico (IQR)

El rango intercuartílico es la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1), y representa la dispersión de la mitad central de los datos.

• Fórmula:
  [ IQR = Q3 – Q1 ]
• Ejemplo: Para el conjunto de datos ordenados: 6, 7, 8, 9, 10, el primer cuartil (Q1) es 7 y el tercer cuartil (Q3) es 9. El rango intercuartílico sería:
  [ 9 – 7 = 2 ]

---

Ejemplo Completo de Métodos Descriptivos

Supongamos que tenemos el siguiente conjunto de datos que representa las puntuaciones obtenidas por 10 estudiantes en un examen:

• Datos: 75, 82, 90, 88, 79, 85, 92, 87, 74, 81
• Media:
  [ \frac{75 + 82 + 90 + 88 + 79 + 85 + 92 + 87 + 74 + 81}{10} = 83.3 ] La media es 83.3.
• Mediana:
  Ordenamos los datos: 74, 75, 79, 81, 82, 85, 87, 88, 90, 92. Como hay un número par de datos, la mediana es el promedio de los dos valores centrales:
  [ \frac{82 + 85}{2} = 83.5 ]
• Moda:
  No hay valor que se repita, por lo tanto, no hay moda en este conjunto de datos.
• Rango:
  [ 92 – 74 = 18 ] El rango es 18.
• Varianza:
  Primero calculamos la media (( \bar{X} = 83.3 )), luego sumamos las diferencias al cuadrado y dividimos entre el número de observaciones:
  [ \text{Varianza} = \frac{(75-83.3)^2 + (82-83.3)^2 + \dots + (81-83.3)^2}{10} = 42.23 ]
• Desviación Estándar:
  [ \sqrt{42.23} = 6.5 ] La desviación estándar es 6.5.

---

Otros Métodos Descriptivos

Además de las medidas numéricas, existen otros métodos descriptivos que se utilizan comúnmente:

a. Tablas de Frecuencia

Las tablas de frecuencia muestran la cantidad de veces que ocurre cada valor o categoría en los datos. Se usan para datos cualitativos o cuantitativos discretos.

• Ejemplo: Si en una encuesta 50 personas respondieron acerca de su deporte favorito, una tabla de frecuencias podría mostrar cuántas personas prefieren fútbol, baloncesto, etc.

b. Gráficos

Los gráficos son herramientas visuales que ayudan a entender rápidamente las características de los datos.

• Histograma: Muestra la distribución de una variable cuantitativa.
• Gráfico de barras: Útil para representar datos cualitativos o discretos.
• Gráfico de cajas y bigotes (Boxplot): Resume la dispersión y detecta posibles outliers.

---

Conclusión

Los métodos descriptivos son fundamentales para un análisis estadístico preliminar, ya que proporcionan información valiosa sobre la estructura y características de los datos. Ya sea mediante medidas de tendencia central, dispersión o mediante gráficos, estos métodos facilitan la comprensión de los patrones y comportamientos de un conjunto de datos.