Redes multicapas

Las Redes Neuronales Multicapa o Multilayer Perceptrons (MLP) son redes neuronales artificiales que incluyen al menos una capa oculta entre la capa de entrada y la capa de salida. La presencia de capas ocultas permite a las MLP aprender patrones complejos y no lineales en los datos, haciendo que estas redes sean adecuadas para resolver problemas complejos de clasificación, regresión y predicción.

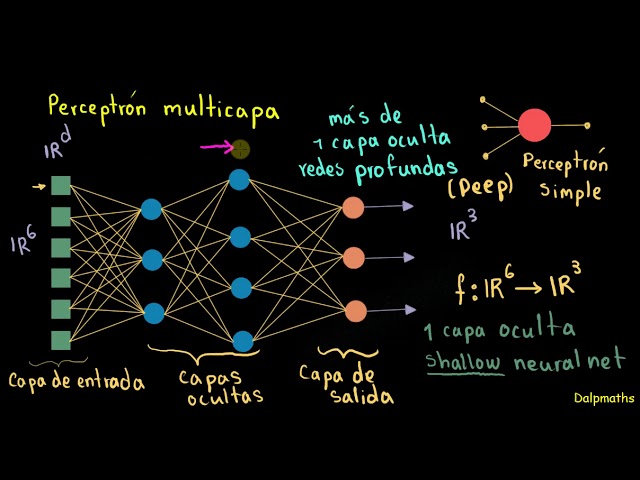
Estructura de una Red Neuronal Multicapa

Las redes MLP se componen de:

1. Capa de Entrada: Recibe los datos de entrada. Cada neurona en esta capa representa una característica de los datos.
2. Capas Ocultas: Procesan y extraen patrones más complejos de los datos. Cuantas más capas ocultas o neuronas haya, mayor será la capacidad de aprendizaje de la red, aunque esto también aumenta el riesgo de sobreajuste.
3. Capa de Salida: Genera el resultado de la red. En problemas de clasificación, la capa de salida puede tener una neurona por cada clase o solo una para problemas binarios.

Cada neurona en una capa está conectada a todas las neuronas de la capa siguiente, formando una red completamente conectada.

Funcionamiento de una Red MLP

En una MLP:

• Las entradas se pasan por la capa de entrada y se multiplican por pesos asociados a cada conexión.
• Las salidas de cada capa se combinan linealmente y pasan por una función de activación (por ejemplo, ReLU, sigmoide, o tanh) que introduce la no linealidad.
• La salida de la red se compara con el valor deseado para calcular el error.
• Usando retropropagación (backpropagation), el error se propaga hacia atrás, ajustando los pesos mediante un algoritmo de optimización (como el descenso de gradiente).

Ejemplo en Python con una Red MLP

En este ejemplo, entrenamos una MLP con scikit-learn para clasificar un conjunto de datos no linealmente separable.

import numpy as np
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# Generar datos de prueba (conjunto no linealmente separable)
X, y = make_moons(n_samples=300, noise=0.2, random_state=42)

# Dividir los datos en conjunto de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Crear y entrenar la red MLP
mlp = MLPClassifier(hidden_layer_sizes=(10, 5), activation='relu', max_iter=1000, random_state=42)
mlp.fit(X_train, y_train)

# Evaluar el modelo
accuracy = mlp.score(X_test, y_test)
print(f"Precisión en el conjunto de prueba: {accuracy:.2f}")

# Visualizar la frontera de decisión
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', edgecolors='k')
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 100), np.linspace(ylim[0], ylim[1], 100))
Z = mlp.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')
plt.title('Clasificación con Red MLP')
plt.xlabel('Característica 1')
plt.ylabel('Característica 2')
plt.show()

Interpretación del Ejemplo

• Datos de Entrada: Se utiliza un conjunto de datos de luna creciente que no es linealmente separable.
• Configuración del MLP: La red tiene dos capas ocultas con 10 y 5 neuronas respectivamente. La función de activación ReLU permite aprender patrones complejos.
• Evaluación: La precisión muestra qué tan bien la red ha aprendido los patrones de los datos.
• Visualización: La frontera de decisión muestra cómo la red divide los datos en función de sus clases.

Características y Limitaciones de las Redes MLP

• Capacidad de aprendizaje: Las MLP pueden aprender patrones complejos debido a la no linealidad introducida por las funciones de activación y las múltiples capas ocultas.
• Sobreajuste: Con muchas neuronas y capas ocultas, la red puede aprender demasiado los datos de entrenamiento, afectando su rendimiento en datos nuevos. El uso de técnicas como la regularización, el dropout o la validación cruzada puede ayudar a mitigar este problema.
• Computación intensiva: Las redes MLP pueden ser computacionalmente intensivas, especialmente con grandes cantidades de datos y configuraciones complejas.

Las MLP son una herramienta básica pero poderosa en redes neuronales y son la base para modelos más complejos como las redes profundas (DNN) y otras arquitecturas avanzadas que integran más capas, unidades convolucionales o recurrentes.

import matplotlib.pyplot as plt
import numpy as np
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# Generar datos de prueba
X, y = make_moons(n_samples=1000, noise=0.2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Escalar los datos para mejorar el rendimiento
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# Crear modelo de red completamente conectada
model = Sequential([
    Dense(10, activation='relu', input_shape=(2,)),  # Primera capa oculta
    Dense(5, activation='relu'),                     # Segunda capa oculta
    Dense(1, activation='sigmoid')                   # Capa de salida (para clasificación binaria)
])

# Compilar el modelo
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# Entrenar el modelo
model.fit(X_train, y_train, epochs=100, validation_data=(X_test, y_test), verbose=1)

# Evaluar el rendimiento
loss, accuracy = model.evaluate(X_test, y_test)
print(f'Precisión en el conjunto de prueba: {accuracy:.2f}')

# Crear una cuadrícula de puntos para visualizar la frontera de decisión
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
grid = np.c_[xx.ravel(), yy.ravel()]
grid_scaled = scaler.transform(grid)

# Predecir sobre la cuadrícula
preds = model.predict(grid_scaled)
preds = preds.reshape(xx.shape)

# Dibujar resultados
plt.figure(figsize=(10, 6))
plt.contourf(xx, yy, preds, cmap="coolwarm", alpha=0.3)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, cmap="coolwarm", edgecolor="k", s=20, label="Datos de Entrenamiento")
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap="coolwarm", edgecolor="k", marker="x", s=20, label="Datos de Prueba")
plt.title("Frontera de decisión de la Red Neuronal Completamente Conectada")
plt.xlabel("Característica 1")
plt.ylabel("Característica 2")
plt.legend()
plt.show()