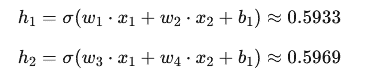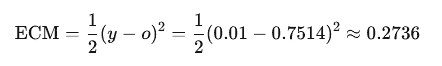Retropropagación

La retropropagación es el método de optimización más utilizado en redes neuronales, y permite ajustar los pesos de cada neurona para reducir el error de predicción. Este algoritmo utiliza el concepto de gradiente descendente, y a través de la derivación y la propagación de errores de una red hacia atrás, ajusta los pesos de las conexiones neuronales para acercarse a un mínimo del error total.

¿Cómo Funciona la Retropropagación?

La retropropagación ocurre en dos fases principales después de obtener la salida de una red neuronal:

1. Propagación Hacia Adelante (Forward Pass):
   • Cada neurona en la red recibe una entrada, la procesa a través de sus pesos y bias y la pasa a través de una función de activación, generando una salida.
   • Esta salida es utilizada en las neuronas de la siguiente capa hasta llegar a la capa final (capa de salida).
   • En la capa de salida, se calcula el error en función de la diferencia entre la predicción y el valor esperado (o etiqueta).
2. Propagación Hacia Atrás (Backward Pass):
   • La retropropagación calcula cómo los cambios en cada peso afectan el error global.
   • Utiliza el gradiente del error con respecto a cada peso, aplicando el principio de la regla de la cadena para derivar el error en relación a los pesos en cada conexión.
   • A medida que este proceso se realiza desde la última capa hacia la primera (hacia atrás), cada peso se actualiza en función del gradiente calculado y una tasa de aprendizaje.

Ejemplo Sencillo de Retropropagación

Imaginemos una red neuronal con:

• Una capa de entrada con 2 neuronas (representan dos características).
• Una capa oculta con 2 neuronas.
• Una capa de salida con 1 neurona (para realizar una predicción binaria).

Usaremos una función de activación Sigmoide ((\sigma(z) = \frac{1}{1 + e^{-z}})).

Supongamos que los valores iniciales son:

• Pesos iniciales:
  • Entre entrada y capa oculta: ( w_1 = 0.15, w_2 = 0.20, w_3 = 0.25, w_4 = 0.30 )
  • Entre capa oculta y salida: ( w_5 = 0.40, w_6 = 0.45 )
• Bias:
  • En la capa oculta: ( b_1 = 0.35 )
  • En la capa de salida: ( b_2 = 0.60 )
• Tasa de aprendizaje: ( \alpha = 0.1 )
• Entrada:
  • ( x_1 = 0.05, x_2 = 0.10 )
  • Salida esperada (label): ( y = 0.01 )

1. Propagación hacia adelante

Calculamos la salida en la capa oculta y luego en la capa de salida:

• Activación de las neuronas en la capa oculta:
• 
• Activación en la neurona de salida:
• 

2. Cálculo del Error

El error se calcula con la función de error cuadrático medio (ECM):

3. Propagación hacia atrás (cálculo de gradientes)

Para minimizar este error, debemos ajustar los pesos en cada conexión. Usamos el gradiente descendente para calcular cómo debe ajustarse cada peso.

Para actualizar ( w_5 ):

• Derivada de la función de error con respecto a ( w_5 ):
• 
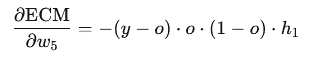
• Calculamos el nuevo valor de ( w_5 ) aplicando:
• 

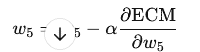
Este proceso se repite para cada peso en cada capa de la red, y así sucesivamente hasta que el error es mínimo.

Ejemplo en Código

import numpy as np
from sklearn.neural_network import MLPClassifier

# Datos de entrenamiento
X = np.array([[0.05, 0.10]])
y = np.array([0])

# Creación de un MLP con una capa oculta
mlp = MLPClassifier(hidden_layer_sizes=(2,), activation='logistic', solver='sgd', learning_rate_init=0.1, max_iter=1)

# Entrenamiento inicial
mlp.partial_fit(X, y, classes=[0, 1])

# Salida del modelo
pred = mlp.predict_proba(X)
print(f"Predicción inicial: {pred}")

# Retropropagación ajustará pesos automáticamente
mlp.partial_fit(X, y)

# Nueva predicción
new_pred = mlp.predict_proba(X)
print(f"Nueva predicción después de retropropagación: {new_pred}")

Interpretación

La retropropagación ha ajustado los pesos para reducir el error entre la predicción inicial y el valor esperado. Con un mayor número de iteraciones (épocas), este proceso se repite, haciendo que la predicción se acerque cada vez más al valor esperado.

Ventajas de la Retropropagación

• Optimización automática: Ajusta pesos y bias para mejorar el modelo.
• Escalabilidad: Se puede aplicar en grandes redes neuronales.
• Flexibilidad: Funciona con funciones de activación variadas (sigmoide, ReLU, etc.).

Limitaciones

• Dependencia de los datos: Para evitar el sobreajuste, requiere grandes volúmenes de datos.
• Costo computacional: Consume recursos y tiempo en redes grandes.

Retropropagación.

https://lamaquinaoraculo.com/deep-learning/la-retropropagacion-del-gradiente/