Tipos de errores

Las medidas de error son fundamentales en estadística y análisis de datos, ya que permiten cuantificar la discrepancia entre los valores observados y los valores predichos o verdaderos. Aquí te explico algunos de los tipos más comunes de medidas de error, junto con su significado, propiedades y ejemplos.

1. Error Absoluto

El error absoluto mide la magnitud de la diferencia entre el valor observado y el valor real. Se calcula de la siguiente manera:

Error Absoluto = |yobservado – yreal|

Propiedades

• No tiene signo, por lo que siempre es positivo.
• Fácil de interpretar, pero no normaliza el error en relación con el valor real.

Ejemplo

Si un valor real es 10 y el valor observado es 8, el error absoluto sería:

[ |8 – 10| = 2 ]

2. Error Cuadrático

El error cuadrático se obtiene elevando al cuadrado el error absoluto. Se utiliza a menudo en contextos donde se busca penalizar errores más grandes.

Error Cuadrático = y(observado) – y(real)^2

Propiedades

• Penaliza más los errores grandes debido a la elevación al cuadrado.
• El resultado es siempre positivo.

Ejemplo

Para los mismos valores anteriores (10 y 8):

[ (8 – 10)^2 = (-2)^2 = 4 ]

3. Error Cuadrático Medio (MSE)

El error cuadrático medio es el promedio de los errores cuadrados. Se utiliza comúnmente en regresiones y modelos predictivos.

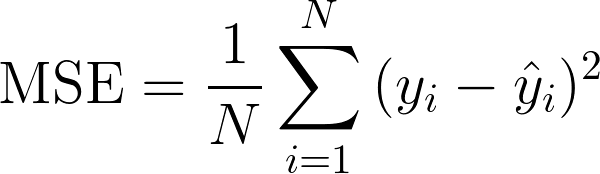
Propiedades

• Proporciona una medida de la calidad del modelo.
• A veces, se usa la raíz cuadrada del MSE, conocida como Root Mean Squared Error (RMSE), para volver a la escala original.

Ejemplo

Supongamos que tenemos los errores cuadrados: 4, 1, y 0:

[ \text{MSE} = \frac{4 + 1 + 0}{3} = \frac{5}{3} \approx 1.67 ]

4. Error Absoluto Medio (MAE)

El error absoluto medio es el promedio de los errores absolutos y proporciona una medida clara de error.

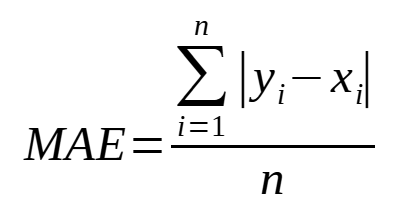
Propiedades

• Se expresa en las mismas unidades que los datos originales.
• Menos sensible a los valores atípicos en comparación con el MSE.

Ejemplo

Si los errores absolutos son 2, 1 y 0:

MAE = (2 + 1 + 0)/3 = 1

5. Error Relativo

El error relativo mide el error en relación con el valor real. Se expresa como un porcentaje.

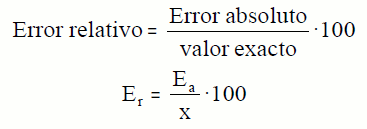
Propiedades

• Proporciona una perspectiva sobre la magnitud del error en relación con el tamaño del valor real.
• Útil cuando se comparan errores en diferentes escalas.

Ejemplo

Con un valor real de 10 y un valor observado de 8:

Error Relativo = |8 – 10|/|10|* 100 =2/10*100 = 20%

6. R2 (Coeficiente de Determinación)

Aunque no es una medida de error en el sentido tradicional, el coeficiente de determinación se utiliza para evaluar la calidad de un modelo de regresión. Indica la proporción de la varianza en la variable dependiente que es predecible a partir de las variables independientes.

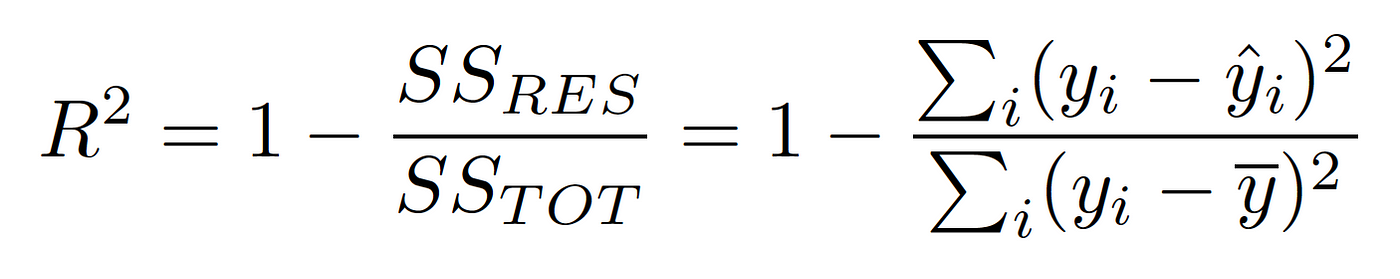
Donde ( SS{res} ) es la suma de los errores al cuadrado y ( SS{tot} ) es la suma total de las diferencias al cuadrado respecto a la media.

Interpretación de R²:

• R² = 0: El modelo no explica nada de la variabilidad de la variable dependiente (Y). Esto significa que el modelo no tiene ninguna capacidad predictiva.
• R² = 1: El modelo explica el 100% de la variabilidad de la variable dependiente. El ajuste del modelo es perfecto (rara vez ocurre en la práctica).
• 0 < R² < 1: El modelo explica parte de la variabilidad de los datos. Cuanto más cercano a 1 esté el valor de R², mejor es el ajuste del modelo.
• R² < 0: Aunque no es común, puede ocurrir en casos donde el modelo tiene un rendimiento muy malo, peor que una línea horizontal de promedio constante. Esto es posible si el modelo no tiene sentido en el contexto de los datos.

Ejemplo de interpretación:

1. R² = 0.85: El modelo de regresión explica el 85% de la variabilidad en los datos. Esto indica que el modelo tiene un buen ajuste, ya que una gran parte de la variabilidad de Y se explica por las variables predictoras.
2. R² = 0.3: El modelo solo explica el 30% de la variabilidad en los datos, lo que significa que es un ajuste relativamente pobre y hay otros factores no modelados que explican gran parte de la variabilidad de Y.
3. R² = 0.95: El modelo explica el 95% de la variabilidad, lo que generalmente se considera un ajuste excelente, aunque también podría ser indicio de sobreajuste (overfitting) si el modelo es muy complejo.

Limitaciones de R²:

• No indica causalidad: Un alto R² no significa necesariamente que las variables independientes estén causando cambios en la variable dependiente.
• No detecta el sobreajuste: Un R² cercano a 1 podría indicar que el modelo está sobreajustando (fitting demasiado los datos de entrenamiento y capturando ruido en lugar de patrones reales).
• No sirve para comparar diferentes tipos de modelos: R² solo es útil dentro de la misma clase de modelos (como regresiones lineales).

 

Resumen

Las medidas de error son fundamentales para evaluar el desempeño de modelos y la calidad de las predicciones. Elegir la medida adecuada depende del contexto y de la naturaleza de los datos, así como de la importancia de los errores en la aplicación específica.